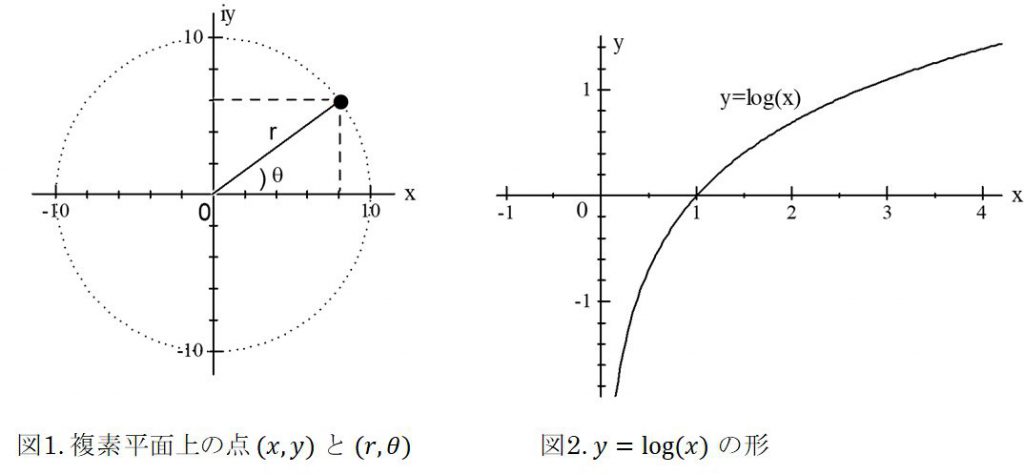
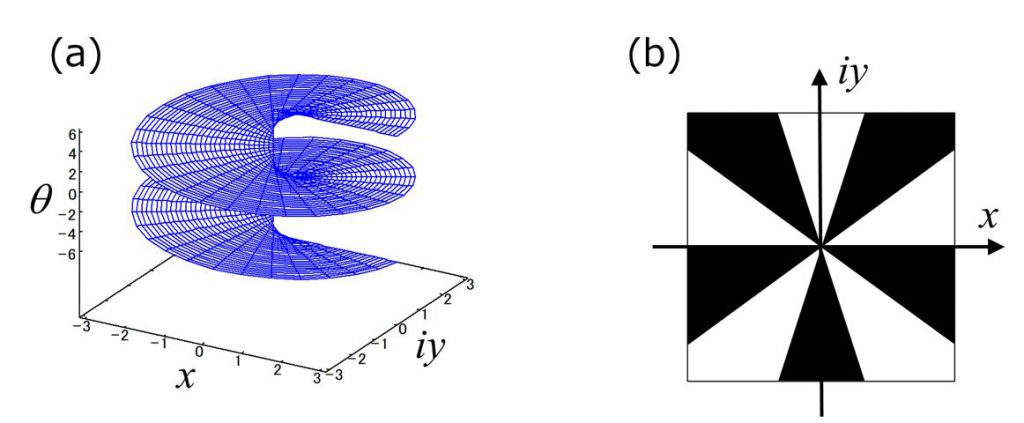
高校の数学で複素数を習っていると思います。虚数を$i$として複素平面$z=x+iy$を考えるのでしたね。この平面上のある点は、座標$(x,y)$を使って書くことができるのですが、その点までの動径$r$と偏角$\theta$を使い、極座標$z = r\text{e}^{i\theta}$で表すこともできます(図1)。一方、$\log$関数も高校で習うのですが、例えば$y = \log(x)$のグラフは図2に示すような形となります。ここで複素数の$\log$関数を考えてみましょう。$\log$関数の中に$z$を入れたものを$w$とすると、$w = \log(z)$なのですが、極座標の形で表記すると$$w = \log(r) +i\theta$$となります。実数の$\log$関数と異なって余計な値$i\theta$がついていますね。この$\theta$は、$z$の平面では極座標における偏角ですので原点を中心に一周すれば元に戻るよ、というものでした。しかし、この$z$の$\log$をとった$w=\log(z)$を考えると、$\theta$が一次関数的に入っていますので、原点の周りを一周しても元に戻らず、1周につき$2\pi i$ずつ値が増加していくことになります。複素数の対数関数$w = \log(z)$の虚数部には$2\pi$の整数倍の多価性があるのです。この様子は、らせん階段を一周回っても元に戻らず、一つ上の階に上るのと似ています(図3(a))。ここで、らせん階段$w =\log(z)$の一周分だけを考え等高線を描いてみましょう。例えば、図3(b)のようになります。でもこの図、放射状に白黒が並んでいるだけで全然らせん階段のように見えませんね。
等高線は、地図を見る上で標高や傾きを知ることができることからとても重要です。しかし、初めての土地の地図は標高が書いていなければどこが山なのか谷なのか分かりませんし、一つ一つの山谷について調べる必要があります(図4(a))。よい方法があります。土地を左右に傾けて、傾けたまま等高線を描くのです。もし、土地が平坦だった場合には上下に真っ直ぐ伸びた等間隔の等高線が描かれます(図4(b))。そしてもし、山や谷があると、山や谷の形を反映しながらも傾けた影響を含めた等高線が描かれます(図4(c))。ここで、この真っ直ぐな等高線(図4(b))を二つ重ね、モアレを見てみましょう。上に重ねた等高線を左右にゆっくりと動かすと一様に明るくなったり暗くなったりします(動画1)。このことからこの等高線で描かれた面は平坦であることが分かります。一方、山や谷のある面を傾けて得た等高線の上に、等間隔の等高線を重ねて動かしてみましょう(動画2)。白になったり黒になったりするタイミングが場所によって異なり、谷から湧き出して山へ向かって収束(或いはその逆)していることが観察できます。即ち、どこが山でどこが谷なのかを動きとして可視化することができるのです。これでどこか1カ所でも山か谷であることが分かれば、全ての領域の山谷が分かりますね。では、先ほどのらせん階段の等高線も描き直してみましょう。らせん階段を傾けて等高線を描いたものが図5(a)です。一様な等高線を上から重ねて左右に動かすと左右に回転することが分かります(動画3)。このモアレの動きから、確かにらせん階段の等高線が描けていることが分かりました。


ところで、この一様な等高線は高校物理に出てくる何かに似てませんか?回折格子です。回折格子とは光が波であるという性質を利用して光を波長毎に分解したり、伝搬の向きを変えるのに使います。らせん階段を傾けて作った等高線もちょっと変な形してしていますが回折格子に見えますね(図5(b))。(この図ではらせん階段を緩やかにしています)この回折格子にレーザーを当てて回折させると、回折光のビームパターンに穴が空くことが分かります(図5(c))。これは、この回折格子の中心の上側と下側では格子の密度が異なるため回折角が異なるものの、右側と左側では中間の回折角であり、それらが様々な方位で滑らかに繋がることでビームが捻れ、光の波面がらせん階段状となるからです。らせん階段の中心は人が通れないのと同様に光も通れず真っ暗となり、穴の空いたストローのようなビームになるわけです。元の$w=\log(z)$に戻った感じですね。このようなビームはラゲールガウスビームと呼ばれ、どんなに小さく絞っても穴は消えず、また、軌道角運動量という性質を持っていることから現在様々な研究が進められています。
文責:東海林
